Generating regular expression from Finite Automata

There are two methods to convert FA to regular expression –
1. State Elimination Method –

• Step 1 –
  If the start state is an accepting state or has transitions in, add a new non-accepting start state and add an €-transition between the new start state and the former start state.
• Step 2 –
  If there is more than one accepting state or if the single accepting state has transitions out, add a new accepting state, make all other states non-accepting, and add an €-transition from each former accepting state to the new accepting state.
• Step 3 –
  For each non-start non-accepting state in turn, eliminate the state and update transitions accordingly.

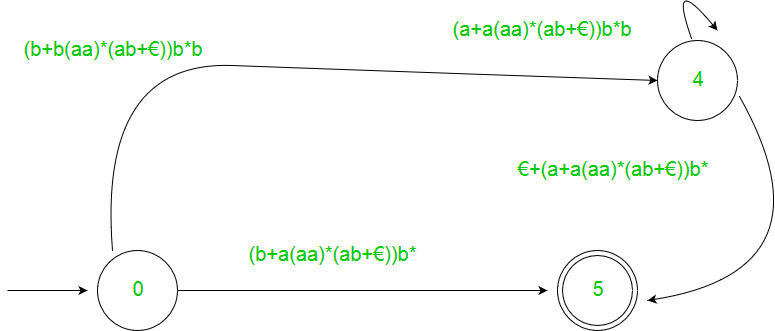
Example :-

 

 

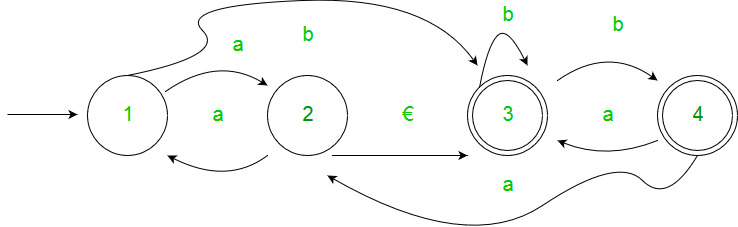
Solution :-
Step 1

Step 2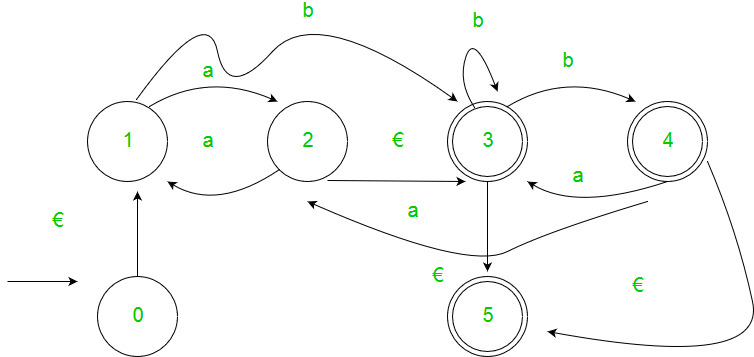

Step 3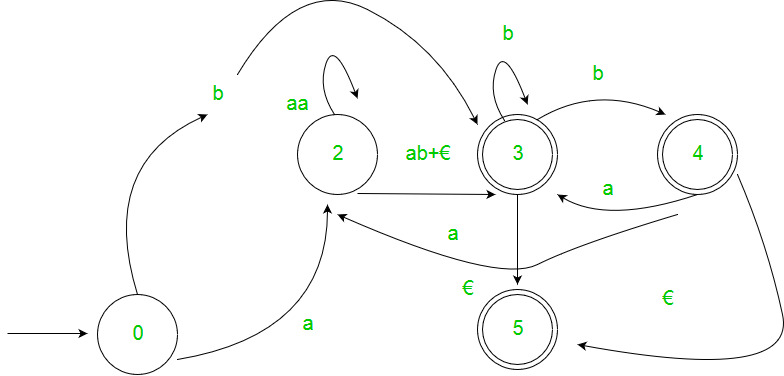

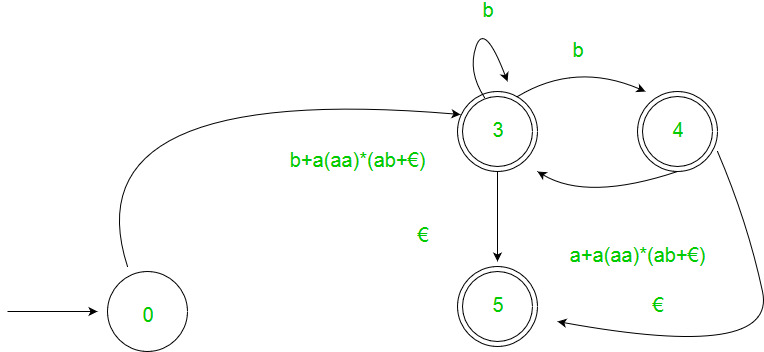
2. Arden’s Theorem – Let P and Q be 2 regular expressions. If P does not contain null string, then following equation in R, viz R = Q + RP, Has a unique solution by R = QP*

Assumptions –

• The transition diagram should not have €-moves.
• It must have only one initial state.

Using Arden’s Theorem to find Regular Expression of Deterministic Finite automata –

1. For getting the regular expression for the automata we first create equations of the given form for all the states
   q₁ = q₁w₁₁ +q₂w₂₁ +…+q_nw_n1 +€ (q₁ is the initial state)
   q₂ = q₁w₁₂ +q₂w₂₂ +…+q_nw_n2
   .
   .
   .
   q_n = q₁w_1n +q₂w_2n +…+q_nw_nn
   
   w_ij is the regular expression representing the set of labels of edges from q_i to q_j

   Note – For parallel edges there will be that many expressions for that state in the expression.

2. Then we solve these equations to get the equation for q_i in terms of w_ij and that expression is the required solution, where q_i is a final state.

Example :-

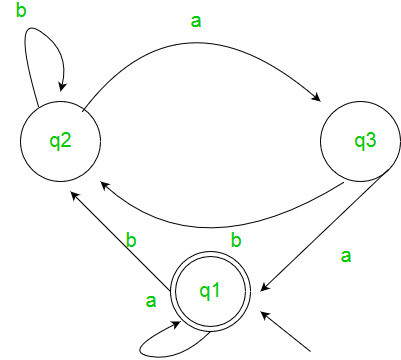
Solution :-
Here the initial state is q₂ and the final state is q₁.
The equations for the three states q₁, q₂, and q₃ are as follows ?
q₁ = q₁a + q₃a + € ( € move is because q₁ is the initial state)
q₂ = q₁b + q₂b + q₃b
q₃ = q₂a
Now, we will solve these three equations ?
q₂ = q₁b + q₂b + q₃b
= q₁b + q₂b + (q₂a)b (Substituting value of q₃)
= q₁b + q₂(b + ab)
= q₁b (b + ab)* (Applying Arden’s Theorem)
q₁ = q₁a + q₃a + €
= q₁a + q₂aa + € (Substituting value of q₃)
= q₁a + q₁b(b + ab*)aa + € (Substituting value of q₂)
= q₁(a + b(b + ab)*aa) + €
= € (a+ b(b + ab)*aa)*
= (a + b(b + ab)*aa)*
Hence, the regular expression is (a + b(b + ab)*aa)*.