Mealy and Moore Machines in TOC

Moore Machines: Moore machines are finite state machines with output value and its output depends only on present state. It can be defined as (Q, q0, ∑, O, δ, λ) where:

• Q is finite set of states.
• q0 is the initial state.
• ∑ is the input alphabet.
• O is the output alphabet.
• δ is transition function which maps Q×∑ → Q.
• λ is the output function which maps Q → O.

Figure 1

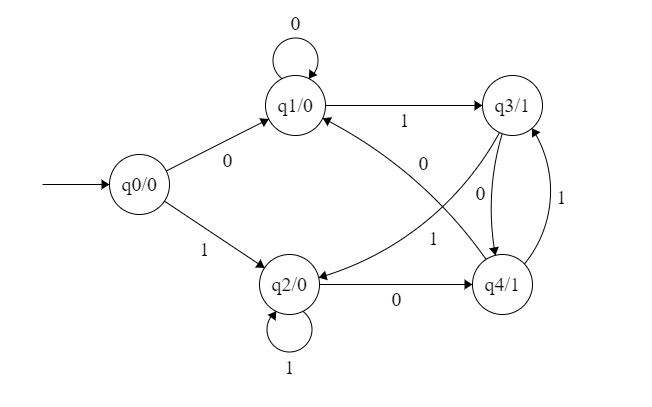
In the moore machine shown in Figure 1, the output is represented with each input state separated by /. The length of output for a moore machine is greater than input by 1.

• Input: 11
• Transition: δ (q0,11)=> δ(q2,1)=>q2
• Output: 000 (0 for q0, 0 for q2 and again 0 for q2)

 Mealy Machines: Mealy machines are also finite state machines with output value and its output depends on present state and current input symbol. It can be defined as (Q, q0, ∑, O, δ, λ’) where:

• Q is finite set of states.
• q0 is the initial state.
• ∑ is the input alphabet.
• O is the output alphabet.
• δ is transition function which maps Q×∑ → Q.
• ‘λ’ is the output function which maps Q×∑→ O.

Figure 2

In the mealy machine shown in Figure 1, the output is represented with each input symbol for each state separated by /. The length of output for a mealy machine is equal to the length of input.

• Input:11
• Transition: δ (q0,11)=> δ(q2,1)=>q2
• Output: 00 (q0 to q2 transition has Output 0 and q2 to q2 transition also has Output 0)

Conversion from Mealy to Moore Machine

Let us take the transition table of mealy machine shown in Figure 2.

	Input=0		Input=1
Present State	Next State	Output	Next State	Output
q0	q1	0	q2	0
q1	q1	0	q2	1
q2	q1	1	q2	0

Table 1

Step 1. First find out those states which have more than 1 outputs associated with them. q1 and q2 are the states which have both output 0 and 1 associated with them.

Step 2. Create two states for these states. For q1, two states will be q10 (state with output 0) and q11 (state with output 1). Similarly for q2, two states will be q20 and q21.

Step 3. Create an empty moore machine with new generated state. For moore machine, Output will be associated to  each state irrespective of inputs.

	Input=0	Input=1
Present State	Next State	Next State	Output
q0
q10
q11
q20
q21

Table 2

Step 4. Fill the entries of next state using mealy machine transition table shown in Table 1. For q0 on input 0,  next state is q10 (q1 with output 0). Similarly, for q0 on input 1, next state is q20 (q2 with output 0). For q1 (both q10 and q11) on input 0, next state is q10. Similarly, for q1(both q10 and q11), next state is q21.  For q10, output will be 0 and  for q11, output will be 1. Similarly, other entries can be filled.

	Input=0	Input=1
Present State	Next State	Next State	Output
q0	q10	q20	0
q10	q10	q21	0
q11	q10	q21	1
q20	q11	q20	0
q21	q11	q20	1

Table 3

This is the transition table of moore machine shown in Figure 1.

Conversion from moore machine to mealy machine

Let us take the moore machine of Figure 1 and its transition table is shown in Table 3.

Step 1. Construct an empty mealy machine using all states of moore machine as shown in Table 4.

	Input=0		Input=1
Present State	Next State	Output	Next State	Output
q0
q10
q11
q20
q21

Table 4

Step 2: Next state for each state can also be directly found from moore machine transition Table as:

	Input=0		Input=1
Present State	Next State	Output	Next State	Output
q0	q10		q20
q10	q10		q21
q11	q10		q21
q20	q11		q20
q21	q11		q20

Table 5

Step 3: As we can see output corresponding to each input in moore machine transition table. Use this to fill the Output  entries. e.g.; Output corresponding to q10, q11, q20 and q21 are 0, 1, 0 and 1 respectively.   

	Input=0		Input=1
Present State	Next State	Output	Next State	Output
q0	q10	0	q20	0
q10	q10	0	q21	1
q11	q10	0	q21	1
q20	q11	1	q20	0
q21	q11	1	q20	0

Table 6

 Step 4:  As we can see from table 6, q10 and q11 are similar to each other (same value of next state and Output for  different Input). Similarly, q20 and q21 are also similar. So, q11 and q21 can be eliminated.

	Input=0		Input=1
Present State	Next State	Output	Next State	Output
q0	q10	0	q20	0
q10	q10	0	q21	1
q20	q11	1	q20	0

Table 7

This is the same mealy machine shown in Table 1. So we have converted mealy to moore machine and converted  back moore to mealy.

Note: Number of states in mealy machine can’t be greater than number  of states in moore machine.

Example: The Finite state machine described by the following state diagram with A as starting state, where an arc label is x / y and x stands for 1-bit input and y stands for 2- bit output?

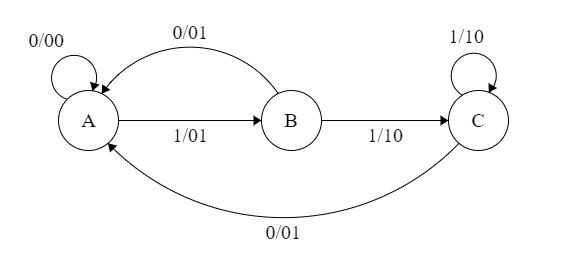
Outputs the sum of the present and the previous bits of the input. 

1. Outputs 01 whenever the input sequence contains 11.
2. Outputs 00 whenever the input sequence contains 10.
3. None of these.

Solution: Let us take different inputs and its output and check which option works:

Input: 01

Output: 00 01  (For 0, Output is 00 and state is A. Then, for 1, Output is 01 and state will be B)

Input: 11

Output: 01 10 (For 1, Output is 01 and state is B. Then, for 1, Output is 10 and state is C)

As we can see, it is giving the binary sum of present and previous bit. For first bit, previous bit is taken as 0.