NP-Completeness | Set 1 (Introduction)

We have been writing about efficient algorithms to solve complex problems, like shortest path, Euler graph, minimum spanning tree, etc. Those were all success stories of algorithm designers. In this post, failure stories of computer science are discussed.

Can all computational problems be solved by a computer? There are computational problems that can not be solved by algorithms even with unlimited time. For example Turing Halting problem (Given a program and an input, whether the program will eventually halt when run with that input, or will run forever). Alan Turing proved that general algorithm to solve the halting problem for all possible program-input pairs cannot exist. A key part of the proof is, Turing machine was used as a mathematical definition of a computer and program (Source Halting Problem).
Status of NP Complete problems is another failure story, NP complete problems are problems whose status is unknown. No polynomial time algorithm has yet been discovered for any NP complete problem, nor has anybody yet been able to prove that no polynomial-time algorithm exist for any of them. The interesting part is, if any one of the NP complete problems can be solved in polynomial time, then all of them can be solved.

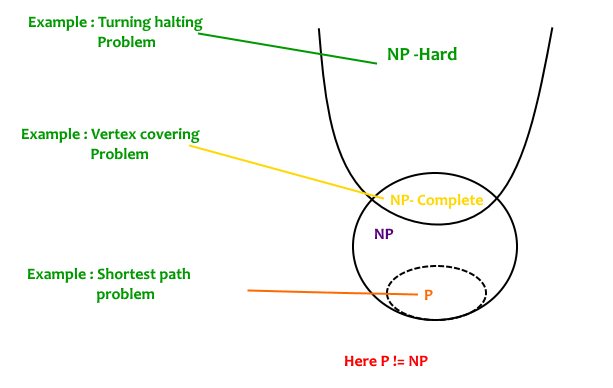
What are NP, P, NP-complete and NP-Hard problems?
P is set of problems that can be solved by a deterministic Turing machine in Polynomial time.

NP is set of decision problems that can be solved by a Non-deterministic Turing Machine in Polynomial time. P is subset of NP (any problem that can be solved by deterministic machine in polynomial time can also be solved by non-deterministic machine in polynomial time).
Informally, NP is set of decision problems which can be solved by a polynomial time via a “Lucky Algorithm”, a magical algorithm that always makes a right guess among the given set of choices (Source Ref 1).

NP-complete problems are the hardest problems in NP set.  A decision problem L is NP-complete if:
1) L is in NP (Any given solution for NP-complete problems can be verified quickly, but there is no efficient known solution).
2) Every problem in NP is reducible to L in polynomial time (Reduction is defined below).

A problem is NP-Hard if it follows property 2 mentioned above, doesn’t need to follow property 1. Therefore, NP-Complete set is also a subset of NP-Hard set.

 

 

Decision vs Optimization Problems
NP-completeness applies to the realm of decision problems.  It was set up this way because it’s easier to compare the difficulty of decision problems than that of optimization problems.   In reality, though, being able to solve a decision problem in polynomial time will often permit us to solve the corresponding optimization problem in polynomial time (using a polynomial number of calls to the decision problem). So, discussing the difficulty of decision problems is often really equivalent to discussing the difficulty of optimization problems. (Source Ref 2).
For example, consider the vertex cover problem (Given a graph, find out the minimum sized vertex set that covers all edges). It is an optimization problem. Corresponding decision problem is, given undirected graph G and k, is there a vertex cover of size k?

What is Reduction?
Let L₁ and L₂ be two decision problems. Suppose algorithm A₂ solves L₂. That is, if y is an input for L₂ then algorithm A₂ will answer Yes or No depending upon whether y belongs to L₂ or not.
The idea is to find a transformation from L₁ to L₂ so that the algorithm A₂ can be part of an algorithm A₁ to solve L₁.

 Learning reduction in general is very important. For example, if we have library functions to solve certain problem and if we can reduce a new problem to one of the solved problems, we save a lot of time. Consider the example of a problem where we have to find minimum product path in a given directed graph where product of path is multiplication of weights of edges along the path. If we have code for Dijkstra’s algorithm to find shortest path, we can take log of all weights and use Dijkstra’s algorithm to find the minimum product path rather than writing a fresh code for this new problem.

How to prove that a given problem is NP complete?
From the definition of NP-complete, it appears impossible to prove that a problem L is NP-Complete.  By definition, it requires us to that show every problem in NP is polynomial time reducible to L.   Fortunately, there is an alternate way to prove it.   The idea is to take a known NP-Complete problem and reduce it to L.  If polynomial time reduction is possible, we can prove that L is NP-Complete by transitivity of reduction (If a NP-Complete problem is reducible to L in polynomial time, then all problems are reducible to L in polynomial time).

What was the first problem proved as NP-Complete?
There must be some first NP-Complete problem proved by definition of NP-Complete problems.  SAT (Boolean satisfiability problem) is the first NP-Complete problem proved by Cook (See CLRS book for proof).

It is always useful to know about NP-Completeness even for engineers. Suppose you are asked to write an efficient algorithm to solve an extremely important problem for your company. After a lot of thinking, you can only come up exponential time approach which is impractical. If you don’t know about NP-Completeness, you can only say that I could not come with an efficient algorithm. If you know about NP-Completeness and prove that the problem as NP-complete, you can proudly say that the polynomial time solution is unlikely to exist. If there is a polynomial time solution possible, then that solution solves a big problem of computer science many scientists have been trying for years.

We will soon be discussing more NP-Complete problems and their proof for NP-Completeness.

References:
MIT Video Lecture on Computational Complexity
Introduction to Algorithms 3rd Edition by Clifford Stein, Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest
http://www.ics.uci.edu/~eppstein/161/960312.html