Operator grammar and precedence parser in TOC

A grammar that is used to define mathematical operators is called an operator grammar or operator precedence grammar. Such grammars have the restriction that no production has either an empty right-hand side (null productions) or two adjacent non-terminals in its right-hand side.

Examples –
This is an example of operator grammar:

E->E+E/E*E/id 

However, the grammar given below is not an operator grammar because two non-terminals are adjacent to each other:

S->SAS/a
A->bSb/b 

We can convert it into an operator grammar, though:

S->SbSbS/SbS/a
A->bSb/b  

Operator precedence parser –
An operator precedence parser is a bottom-up parser that interprets an operator grammar. This parser is only used for operator grammars. Ambiguous grammars are not allowed in any parser except operator precedence parser.
There are two methods for determining what precedence relations should hold between a pair of terminals:

1. Use the conventional associativity and precedence of operator.
2. The second method of selecting operator-precedence relations is first to construct an unambiguous grammar for the language, a grammar that reflects the correct associativity and precedence in its parse trees.

This parser relies on the following three precedence relations: ⋖, ≐, ⋗
a ⋖ b This means a “yields precedence to” b.
a ⋗ b This means a “takes precedence over” b.
a ≐ b This means a “has same precedence as” b.

Figure – Operator precedence relation table for grammar E->E+E/E*E/id

There is not given any relation between id and id as id will not be compared and two variables can not come side by side. There is also a disadvantage of this table – if we have n operators then size of table will be n*n and complexity will be 0(n²). In order to decrease the size of table, we use operator function table.

Operator precedence parsers usually do not store the precedence table with the relations; rather they are implemented in a special way. Operator precedence parsers use precedence functions that map terminal symbols to integers, and the precedence relations between the symbols are implemented by numerical comparison. The parsing table can be encoded by two precedence functions f and g that map terminal symbols to integers. We select f and g such that:

1. f(a) < g(b) whenever a yields precedence to b
2. f(a) = g(b) whenever a and b have the same precedence
3. f(a) > g(b) whenever a takes precedence over b

Example – Consider the following grammar:

 E -> E + E/E * E/( E )/id   

This is the directed graph representing the precedence function:

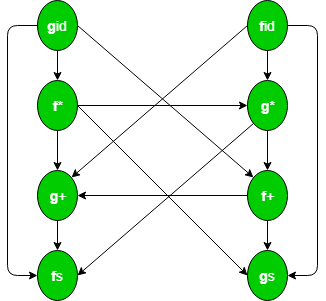
Since there is no cycle in the graph, we can make this function table:

fid -> g* -> f+ ->g+ -> f$
gid -> f* -> g* ->f+ -> g+ ->f$ 

Size of the table is 2n.

One disadvantage of function tables is that even though we have blank entries in relation table we have non-blank entries in function table. Blank entries are also called error. Hence error detection capability of relation table is greater than function table.

#include<stdlib.h> #include<stdio.h> #include<string.h>    // function f to exit from the loop // if given condition is not true void f() {     printf("Not operator grammar");     exit(0); }    void main() {     char grm[20][20], c;        // Here using flag variable,     // considering grammar is not operator grammar     int i, n, j = 2, flag = 0;        // taking number of productions from user     scanf("%d", &n);     for (i = 0; i < n; i++)         scanf("%s", grm[i]);        for (i = 0; i < n; i++) {         c = grm[i][2];            while (c != '\0') {                if (grm[i][3] == '+' || grm[i][3] == '-'                 || grm[i][3] == '*' || grm[i][3] == '/')                    flag = 1;                else {                    flag = 0;                 f();             }                if (c == '$') {                 flag = 0;                 f();             }                c = grm[i][++j];         }     }        if (flag == 1)         printf("Operator grammar"); }

Input :3
A=A*A
B=AA
A=$

Output : Not operator grammar

Input :2
A=A/A
B=A+A

Output : Operator grammar

$ is a null production here which are also not allowed in operator grammars.

Advantages –

1. It can easily be constructed by hand.
2. It is simple to implement this type of parsing.

Disadvantages –

1. It is hard to handle tokens like the minus sign (-), which has two different precedence (depending on whether it is unary or binary).
2. It is applicable only to a small class of grammars.